"Второй признак равенства треугольников"
Автор:
Лефанова Наталья Анатольевна,
учитель математики,
МБОУ СОШ №1,
г.Павлово Нижегородской области.
План-конспект урока геометрии в 7-м классе
(с использованием технологии системно-деятельностного подхода)
.
Цели урока:
1. Содержательная:
* с помощью практических знаний обеспечить понимание учащимися отличия между первым и вторым признаками равенства треугольников,
а также между определением равных треугольников и признаком равенства треугольников.
2. Деятельностная:
* формировать у учащихся навыки доказательства утверждений с помощью ранее изученных понятий и теорем.;
* формировать у учащихся умения применять второй признак равенства при определении равенства треугольников;
3. Развивающая:
* формировать ключевые компетенции учащихся: информационную (умение анализировать информацию, сравнивать, делать выводы),
проблемную (умение ставить проблемы и с помощью имеющихся знаний находить выход из ситуации); коммуникативную
( умение работать в группах, умение слушать и слышать других, принимать мнение других)
Результаты обучения:
На данном уроке учащиеся должны:
* усвоить признак равенства треугольников по стороне и двум прилежащим к ней углам;
* усвоить алгоритм доказательства первого признака равенства треугольников;
* научиться находить в задаче равные элементы и использовать их при применении второго признака;
Содержание учебного материала: второй признак равенства треугольников и простейшие задачи на его применение.
Единица содержания образования:
* способ доказательства теоремы - наложение треугольников;
* способ решение задачи- анализ данных ( равные стороны и прилежащие к ним углы) и применение второго признака равенства треугольников.
Подготовительный этап.
Шаг 1. Мотивирование.
Слайд №1: план урока:
* Я уже умею?
* Я хочу узнать?
* Я узнаю сам!
* Попробую применить!
* Я справлюсь!
* Мои успехи.
* Что мне предстоит?
Сегодня вы поставите каждый себе оценку в карточке самооценки.
Самооценка работы на уроке:

Итак, начнем урок с первого пункта плана:
1. Вопросы для устной работы:
> Какие треугольники называются равными?
> Как можно узнать, равны ли данные треугольники? (наложением и по первому признаку равенства треугольников)
Ø Какие элементы достаточно рассмотреть для доказательства равенства треугольников? ( две стороны и угол между ними)
Ø Сформулируйте первый признак равенства треугольников.
2. Решение задач по готовым чертежам.
Слайд № 2,3: Задача 1. ( с краткой записью решения)
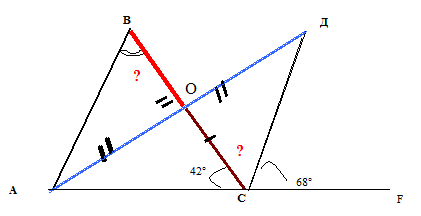
> Можем ли мы сразу найти угол АВО?
> Равенство каких треугольников мы можем доказать?
> Что последует из равенства треугольников?
> Как найти угол ОСД?
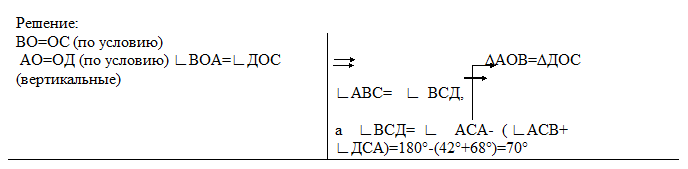
Сравнение решения с эталоном. ( эталон записан на доске)
* Какие равные элементы треугольников мы использовали для доказательства равенства ΔАОВ и ΔДОС?
* Равенство каких элементов нам понадобилось для последующего решения задачи?
3.Самооценка этапа урока.
Оцените свое решение с эталоном ( мах=3 б)
Шаг 2. Актуализация опорных знаний и выдвижение гипотезы; фиксирование затруднения
в пробном действии, определение границы между знанием и незнанием.
Слайд 4, 5: Задача 2. С помощью транспортира и линейки постройте треугольник АВС, в котором
∟А=45°, ∟С=75°, АВ=6см.
Можно ли задать алгоритм построения для такого треугольника?
Что нужно поменять в данных, чтобы треугольник можно было построить? ( Задать величину угла В=75°)
* Какие шаги выполнить при построении?
1. Строим отрезок АВ
2. Строим ∟А=45°
3. Строим ∟В=75°
* Измерим стороны ВС и АС. Какие длины у вас получились? ( АС=7 см; ВС=5,5 см.)
* Можно ли воспользоваться этим алгоритмом для построения треугольника, у которого известны?
Шаг3. Постановка учащимися цели урока как собственной учебной задачи.
Вопросы учащимся:
* Почему у всех получились равные стороны?
* Что можно сказать о ваших построенных треугольниках?
* Почему же получились равные треугольники?
* Какой же признак равенства вы можете сформулировать?
Гипотезе: треугольники равны, если у них равна одна сторона и два угла.
Учащиеся ставят перед собой цели:
> Выяснить по какому еще признаку можно судить о равенстве треугольников?
> Доказать или опровергнуть собственную гипотезу равенства двух треугольников по сторона и двум углам.
> Научиться применять новый признак при решении задач.
Основной этап – открытие новых знаний. ( Слайд 6,7)
Шаг4. Разработка проекта выхода из затруднений.
1. Попробуем доказать или опровергнуть наше предположение.
2. Выполним чертеж.
3. Запишем, что дано и что требуется доказать.
4. Каким способом будем доказывать наше утверждение? ( наложением)
5. Обсуждение в группах : составить алгоритм действий при наложении треугольников
Шаг5. Реализация готового проекта - открытие новых знаний
Учащиеся после обсуждения в группах выполняют доказательство признака, выполняя по очереди пункты плана доказательства признака.
Алгоритм действий:
1. Вершину А совместим с вершиной А1.
2. Наложить сторону АВ на сторону А1В1.
3. Угол ВАС совместится с углом В1А1С1
4. Угол АВС совместится с углом А1В1С1
5. Вершина С совместится с вершиной С1.
Шаг6. Первичное закрепление с проговариванием во внешней речи.
1. Прочитать признак в учебнике.
2. Проговорить в парах формулировку теоремы
3. Проговорить формулировку и доказательство теоремы.( сильный учащийся)
Заключительный этап –применение знаний и рефлексия.
Шаг7 . Включение в систему знаний и повторение.
Задача 3.
Доказать , что Δ АВС и Δ А1В1С1 равны, если АВ= А1В1, ∟А= ∟А1;
∟С= ∟С1. ( по готовому чертежу)
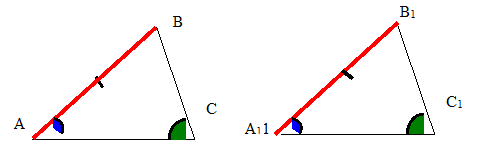
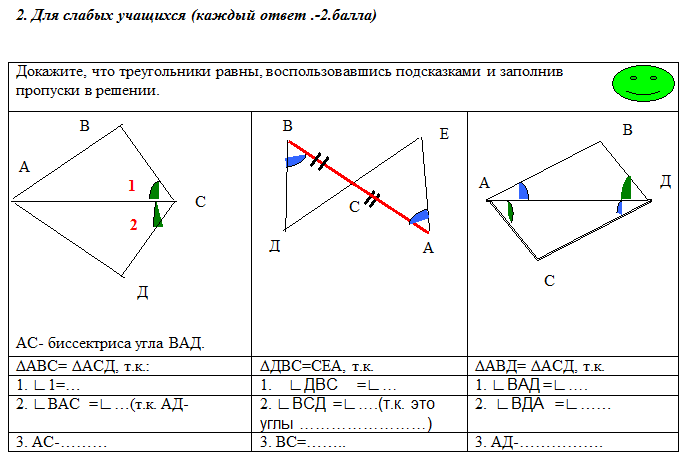
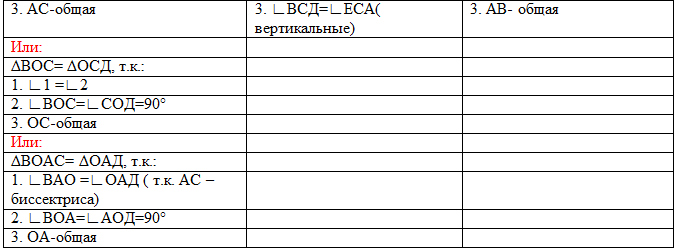
Шаг8. Дифференцированная самостоятельная работа. ( по готовым чертежам с самопроверкой по эталону ответа) (Слайд 8,9)
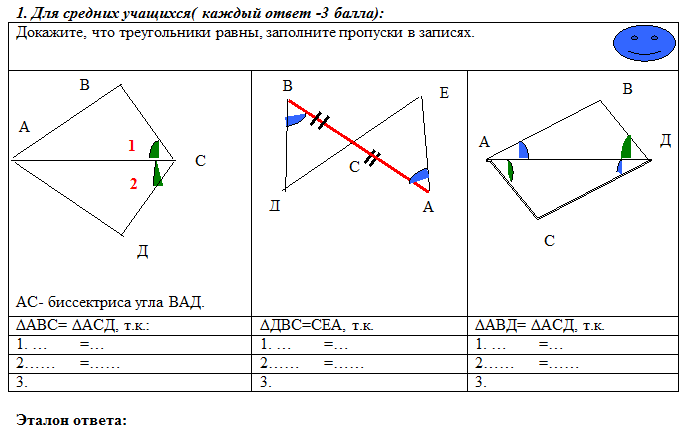
По готовым чертежам заполнить таблицу:
> Оценить по эталону ответа самостоятельную работу, выставив в таблицу самооценки по одному баллу за каждую правильно решенную задачу. ( макс.- 3 балла)



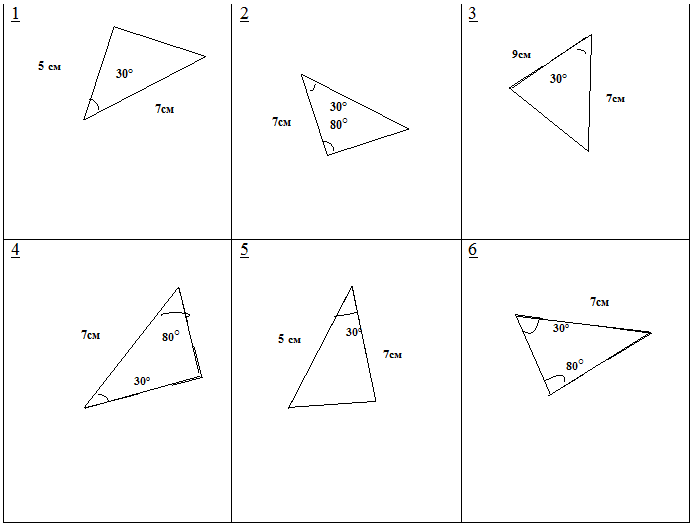
Шаг9. Рефлексия учебной деятельности (Слайд 10)
Экспресс-диагностика: найдите на чертеже равные треугольники:

Использованная литература:
1. Геометрия 7-9, Л.С. Атанасян, М.- Просвещение, 2010.
2. Л. Г. Петерсон: «Интегративная технология развивающего обучения», Москва: НИИ школьных технологий, 2006.
3. Л. Г. Петерсон: Программа для апробации надпредметного курса «Мир деятельности», М.; «Просвещение», 2010.



